
Zadanie Proste (pro)
Pomóż nam usprawnić bazę zadań!
Proste
Limit pamięci: 32 MB
Dane jest sześć liczb cał kowitych  ,
,  ,
,  ,
,  ,
,
 ,
,  takich, że
takich, że 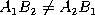 .
Liczby te oznaczają równania dwóch prostych przecinających się:
.
Liczby te oznaczają równania dwóch prostych przecinających się:
 ,
, .
.
 ,
,  ).
Mając dany punkt o współrzędnych całkowitych
).
Mając dany punkt o współrzędnych całkowitych  reprezentujący jedną część, należy podać taki punkt o
współrzędnych całkowitych
reprezentujący jedną część, należy podać taki punkt o
współrzędnych całkowitych  reprezentujący tę samą część,
którego odległość od punktu przecięcia prostych
reprezentujący tę samą część,
którego odległość od punktu przecięcia prostych  i
i  jest
najmniejsza.
jest
najmniejsza.
Zadanie
Napisz program, który:
-
Wczyta ze standardowego wejścia równania prostych
 i
i  oraz
punkt reprezentujący jedną część.
oraz
punkt reprezentujący jedną część.
-
Znajdzie punkt o współrzędnych całkowitych reprezentujący
daną część, który jest najbliższy punktowi przecięcia
prostych
 i
i  .
.
- Wypisze wynik na standardowe wyjście.
Wejście
Pierwszy wiersz standardowego wejścia zawiera trzy liczby
 pooddzielane pojedynczymi odstępami -
współczynniki równania prostej
pooddzielane pojedynczymi odstępami -
współczynniki równania prostej  .
Drugi wiersz zawiera trzy liczby
.
Drugi wiersz zawiera trzy liczby  pooddzielane
pojedynczymi odstępami - współczynniki równania prostej
pooddzielane
pojedynczymi odstępami - współczynniki równania prostej  .
Dla tych liczb zachodzi
.
Dla tych liczb zachodzi  .
Trzeci i ostatni wiersz zawiera dwie liczby całkowite
.
Trzeci i ostatni wiersz zawiera dwie liczby całkowite  oddzielone pojedynczym odstępem - współrzędne punktu
reprezentującego jedną część.
Punkt
oddzielone pojedynczym odstępem - współrzędne punktu
reprezentującego jedną część.
Punkt  nie leży na żadnej z prostych
nie leży na żadnej z prostych  i
i  .
Dla każdej liczby
.
Dla każdej liczby  z wejścia spełnione jest
z wejścia spełnione jest
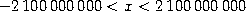 .
.
Wyjście
Twój program powinien wypisać na standardowe wyjście dwie liczby
 oddzielone pojedynczym odstępem - współrzędne punktu
oddzielone pojedynczym odstępem - współrzędne punktu
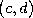 reprezentującego daną część, którego odległość od punktu
przecięcia prostych
reprezentującego daną część, którego odległość od punktu
przecięcia prostych  i
i  jest najmniejsza.
W przypadku, gdy istnieje wiele takich punktów, Twój program
powinien wypisać tylko jeden z nich.
jest najmniejsza.
W przypadku, gdy istnieje wiele takich punktów, Twój program
powinien wypisać tylko jeden z nich.
Przykład
Dla danych wejściowych:1 -1 1 2 -3 1 5 4poprawną odpowiedzią jest:
2 2

Autor zadania: Jakub Pawlewicz.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English